GnomμΣπry θέ ΠΓΣΣ of all roots Ρέακ ιν Γ ιν Σπρινγκ where the spring is sprung again and agin

The same concept appears several times in MS 3052 # 1 (Friberg, 2007, 258) where the change in the width per unit height is called indanum. A 

trapezoid with height h and parallel sides of length a and b, where �

$<�$, thus has an indanum of

 β - α / η  $\frac{-�}{ℎ}.$This appears strange to thinkiers in solid shapes and rocks ηot to water people who think in terms of air which is no more than gaseous water and so both shapes  combine the ukullû (or slopes) of two slanting sides, and so is a

 feature of the entire shape

 rather than a feature or α φέατυρε of one of its sides...:.. The two trapezoids in Figure 3, for example, have the same indanum.

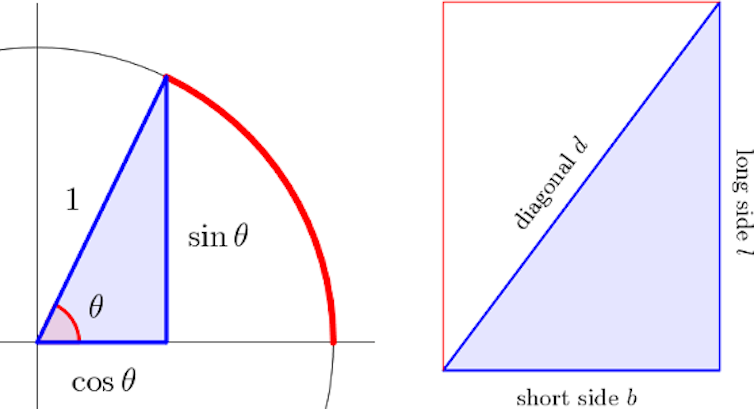
3.1. The Diagonal rule

Evidence of the Diagonal rule, which now we call Pythagoras' theorem, can be found in quite a few tablets (Høyrup, 1999, 396–401; Melville, 2004, 150–152; Friberg, 2007, 450). This demonstrates the crucial metrical understanding that the three sides of a right triangle, or the sides and diagonal of a rectangle, $(�,�,�)$ are related by the equation${�}^2+{�}^2={�}^2.$

Right triangles and rectangles of unit height $�=1$ appear to have been particularly significant, and we call a right triangle (or rectangle) with sides $(�,1,�)$ normalized when β and δ are sexagesimal numbers. These quantities notably capture the ratios involved in a corresponding un-normalized similar right triangle. For a normalized right triangle this is naturally connected to the idea of ukullû, while for a normalized rectangle β is a “statement of the relative flatness of the rectangles” (Britton et al., 2011, 539).

3 4 5 is a pithagorean triple

1+1=2

2x2=4

4+2=6

6/2=3

3x3=9

4x4=16

16+9=25

25/5=5

fifteen rows of these are those on the plimpton

322

Circumcircle of a triangle

A circle which passes through all three vertices of a triangle
Also "Circumscribed circle".

Try this Drag the orange dots on each vertex to reshape the triangle. Note that the circumcircle always passes through all three points.

Hide

|<    >|

RESET

Circumcircle radius

=

11.59

The circumcircle always passes through all three vertices of a triangle. Its center is at the point where all the perpendicular bisectors of the triangle's sides meet. This center is called the circumcenter. See circumcenter of a triangle for more about this.

Note that the center of the circle can be inside or outside of the triangle. Adjust the triangle above and try to obtain these cases.

The radius of the circumcircle is also called the triangle's circumradius.

For right triangles

In the case of a right triangle, the hypotenuse is a diameter of the circumcircle, and its center is exactly at the midpoint of the hypotenuse. 

This is the same situation as Thales Theorem

where the diameter

 subtends a right angle

 to any point

 on a circled circumference.

If you drag the triangle in the figure above you can create this same situation.

 The side of the Great Pyramid at Giza had an original height of 280 cubits and a width of base of 440 cubits. What was the length z of an edge of the pyramid (from a corner to the top)?

Since half of the base

 would be 220 cubits 

 the seqed or ukullû of 

the side of 

the pyramid 

would have been 

220:280

5 1/2 : 7

5 palms and 2 fingers per cubit. 

 to get at the edge of the pyramid, we must use a triangle of height 280

 and approximate base 220 x sqrtf(2)

Babylonian trigonometry

The Babylonians discovered their own unique form of trigonometry during the Old Babylonian period (1900-1600BCE), more than 1,500 years earlier than the Greek form.

Remarkably, their trigonometry contains none of the hallmarks of our modern trigonometry - it does not use angles and it does not use approximation.

The Babylonians had a completely different conceptualisation of a right triangle. They saw it as half of a rectangle, and due to their sophisticated sexagesimal (base 60) number system they were able to construct a wide variety of right triangles using only exact ratios.