Orbital angular velocity οφ Ευσελες Ιδέας

 

Parametric equation

From Wikipedia, the free encyclopedia

(Redirected from Parametric curve)

Jump to navigationJump to search

The butterfly curve can be defined by parametric equations of x and y.

In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters.^[1] Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, in which case the equations are collectively called a parametric representation or parameterization (alternatively spelled as parametrisation) of the object.^[1][2][3]

For example, the equations

${\displaystyle {\begin{aligned}x&=\cos t\\y&=\sin t\end{aligned}}}$

form a parametric representation of the unit circle, where t is the parameter: A point (x, y) is on the unit circle if and only if there is a value of t such that these two equations generate that point. Sometimes the parametric equations for the individual scalar output variables are combined into a single parametric equation in vectors:

${\displaystyle (x,y)=(\cos t,\sin t).}$

Parametric representations are generally nonunique (see the "Examples in two dimensions" section below), so the same quantities may be expressed by a number of different parameterizations.^[1]

In addition to curves and surfaces, parametric equations can describe manifolds and algebraic varieties of higher dimension, with the number of parameters being equal to the dimension of the manifold or variety, and the number of equations being equal to the dimension of the space in which the manifold or variety is considered (for curves the dimension is one and one parameter is used, for surfaces dimension two and two parameters, etc.).

Parametric equations are commonly used in kinematics, where the trajectory of an object is represented by equations depending on time as the parameter. Because of this application, a single parameter is often labeled t; however, parameters can represent other physical quantities (such as geometric variables) or can be selected arbitrarily for convenience. Parameterizations are non-unique; more than one set of parametric equations can specify the same curve.^[4]

Contents

• 1Applications
  • 1.1Kinematics
  • 1.2Computer-aided design
  • 1.3Integer geometry
• 2Implicitization
• 3Examples in two dimensions
  • 3.1Parabola
  • 3.2Explicit equations
  • 3.3Circle
  • 3.4Ellipse
  • 3.5Lissajous Curve
  • 3.6Hyperbola
  • 3.7Hypotrochoid
  • 3.8Some sophisticated functions
• 4Examples in three dimensions
  • 4.1Helix
  • 4.2Parametric surfaces
• 5Examples with vectors
• 6See also
• 7Notes
• 8External links

Applications[edit]

Kinematics[edit]

In kinematics, objects' paths through space are commonly described as parametric curves, with each spatial coordinate depending explicitly on an independent parameter (usually time). Used in this way, the set of parametric equations for the object's coordinates collectively constitute a vector-valued function for position. Such parametric curves can then be integrated and differentiated termwise. Thus, if a particle's position is described parametrically as

${\displaystyle \mathbf {r} (t)=(x(t),y(t),z(t))}$

then its velocity can be found as

${\displaystyle \mathbf {v} (t)=\mathbf {r} '(t)=(x'(t),y'(t),z'(t))}$

and its acceleration as

${\displaystyle \mathbf {a} (t)=\mathbf {r} ''(t)=(x''(t),y''(t),z''(t))}$.

Computer-aided design[edit]

Another important use of parametric equations is in the field of computer-aided design (CAD).^[5] For example, consider the following three representations, all of which are commonly used to describe planar curves.

Type	Form	Example	Description
Explicit	${\displaystyle y=f(x)\,\!}$	${\displaystyle y=mx+b\,\!}$	Line
Implicit	${\displaystyle f(x,y)=0\,\!}$	${\displaystyle \left(x-a\right)^{2}+\left(y-b\right)^{2}=r^{2}}$	Circle
Parametric	${\displaystyle x={\frac {g(t)}{w(t)}};\,\!}$ ${\displaystyle y={\frac {h(t)}{w(t)}}}$	${\displaystyle x=a_{0}+a_{1}t;\,\!}$ ${\displaystyle y=b_{0}+b_{1}t\,\!}$	Line
		${\displaystyle x=a+r\,\cos t;\,\!}$ ${\displaystyle y=b+r\,\sin t\,\!}$	Circle

Each representation has advantages and drawbacks for CAD applications.

The explicit representation may be very complicated, or even may not exist. Moreover, it does not behave well under geometric transformations, and in particular under rotations. On the other hand, as a parametric equation and an implicit equation may easily be deduced from an explicit representation, when a simple explicit representation exists, it has the advantages of both other representations.

Implicit representations may make it difficult to generate points on the curve, and even to decide whether there are real points. On the other hand, they are well suited for deciding whether a given point is on a curve, or whether it is inside or outside of a closed curve.

Such decisions may be difficult with a parametric representation, but parametric representations are best suited for generating points on a curve, and for plotting it.^[6]

Integer geometry[edit]

Numerous problems in integer geometry can be solved using parametric equations. A classical such solution is Euclid's parametrization of right triangles such that the lengths of their sides a, b and their hypotenuse c are coprime integers. As a and b are not both even (otherwise a, b and c would not be coprime), one may exchange them to have a even, and the parameterization is then

${\displaystyle a=2mn,\ \ b=m^{2}-n^{2},\ \ c=m^{2}+n^{2},}$

where the parameters m and n are positive coprime integers that are not both odd.

By multiplying a, b and c by an arbitrary positive integer, one gets a parametrization of all right triangles whose three sides have integer lengths.

Orbital angular velocity of a point particle[edit source]

Particle in two dimensions[edit source]

The angular velocity of the particle at P with respect to the origin O is determined by the perpendicular component of the velocity vector v.

In the simplest case of circular motion at radius ${\displaystyle r}$, with position given by the angular displacement ${\displaystyle \phi (t)}$ from the x-axis, the orbital angular velocity is the rate of change of angle with respect to time: ${\textstyle \omega ={\frac {d\phi }{dt}}}$. If ${\displaystyle \phi }$ is measured in radians, the arc-length from the positive x-axis around the circle to the particle is ${\displaystyle \ell =r\phi }$, and the linear velocity is ${\textstyle v(t)={\frac {d\ell }{dt}}=r\omega (t)}$, so that ${\textstyle \omega ={\frac {v}{r}}}$.

In the general case of a particle moving in the plane, the orbital angular velocity is the rate at which the position vector relative to a chosen origin "sweeps out" angle. The diagram shows the position vector ${\displaystyle \mathbf {r} }$ from the origin ${\displaystyle O}$ to a particle ${\displaystyle P}$, with its polar coordinates ${\displaystyle (r,\phi )}$. (All variables are functions of time ${\displaystyle t}$.) The particle has linear velocity splitting as ${\displaystyle \mathbf {v} =\mathbf {v} _{\|}+\mathbf {v} _{\perp }}$, with the radial component ${\displaystyle \mathbf {v} _{\|}}$ parallel to the radius, and the cross-radial (or tangential) component ${\displaystyle \mathbf {v} _{\perp }}$ perpendicular to the radius. When there is no radial component, the particle moves around the origin in a circle; but when there is no cross-radial component, it moves in a straight line from the origin. Since radial motion leaves the angle unchanged, only the cross-radial component of linear velocity contributes to angular velocity.

The angular velocity ω is the rate of change of angular position with respect to time, which can be computed from the cross-radial velocity as:

${\displaystyle \omega ={\frac {d\phi }{dt}}={\frac {v_{\perp }}{r}}.}$

Here the cross-radial speed ${\displaystyle v_{\perp }}$ is the signed magnitude of ${\displaystyle \mathbf {v} _{\perp }}$, positive for counter-clockwise motion, negative for clockwise. Taking polar coordinates for the linear velocity ${\displaystyle \mathbf {v} }$ gives magnitude ${\displaystyle v}$ (linear speed) and angle ${\displaystyle \theta }$ relative to the radius vector; in these terms, ${\displaystyle v_{\perp }=v\sin(\theta )}$, so that

${\displaystyle \omega ={\frac {v\sin(\theta )}{r}}.}$

These formulas may be derived doing ${\displaystyle \mathbf {r} =(r\cos(\varphi ),r\sin(\varphi ))}$, being ${\displaystyle r}$ a function of the distance to the origin with respect to time, and ${\displaystyle \varphi }$ a function of the angle between the vector and the x axis. Then ${\textstyle {\frac {d\mathbf {r} }{dt}}=({\dot {r}}\cos(\varphi )-r{\dot {\varphi }}\sin(\varphi ),{\dot {r}}\sin(\varphi )+r{\dot {\varphi }}\cos(\varphi ))}$. Which is equal to ${\displaystyle {\dot {r}}(\cos(\varphi ),\sin(\varphi ))+r{\dot {\varphi }}(-\sin(\varphi ),\cos(\varphi ))={\dot {r}}{\hat {r}}+r{\dot {\varphi }}{\hat {\varphi }}}$. (See Unit vector in cylindrical coordinates). Knowing ${\textstyle {\frac {d\mathbf {r} }{dt}}=\mathbf {v} }$, we conclude that the radial component of the velocity is given by ${\displaystyle {\dot {r}}}$, because ${\displaystyle {\hat {r}}}$ is a radial unit vector; and the perpendicular component is given by ${\displaystyle r{\dot {\varphi }}}$ because ${\displaystyle {\hat {\varphi }}}$ is a perpendicular unit vector.

In two dimensions, angular velocity is a number with plus or minus sign indicating orientation, but not pointing in a direction. The sign is conventionally taken to be positive if the radius vector turns counter-clockwise, and negative if clockwise. Angular velocity then may be termed a pseudoscalar, a numerical quantity which changes sign under a parity inversion, such as inverting one axis or switching the two axes.

Particle in three dimensions[edit source]

The orbital angular velocity vector encodes the time rate of change of angular position, as well as the instantaneous plane of angular displacement. In this case (counter-clockwise circular motion) the vector points up.

In three-dimensional space, we again have the position vector r of a moving particle. Here, orbital angular velocity is a pseudovector whose magnitude is the rate at which r sweeps out angle, and whose direction is perpendicular to the instantaneous plane in which r sweeps out angle (i.e. the plane spanned by r and v). However, as there are two directions perpendicular to any plane, an additional condition is necessary to uniquely specify the direction of the angular velocity; conventionally, the right-hand rule is used.

Let the pseudovector ${\displaystyle \mathbf {u} }$ be the unit vector perpendicular to the plane spanned by r and v, so that the right-hand rule is satisfied (i.e. the instantaneous direction of angular displacement is counter-clockwise looking from the top of ${\displaystyle \mathbf {u} }$). Taking polar coordinates ${\displaystyle (r,\phi )}$ in this plane, as in the two-dimensional case above, one may define the orbital angular velocity vector as:

${\displaystyle {\boldsymbol {\omega }}=\omega \mathbf {u} ={\frac {d\phi }{dt}}\mathbf {u} ={\frac {v\sin(\theta )}{r}}\mathbf {u} ,}$

where θ is the angle between r and v. In terms of the cross product, this is:

${\displaystyle {\boldsymbol {\omega }}={\frac {\mathbf {r} \times \mathbf {v} }{r^{2}}}.}$^[4]

From the above equation, one can recover the tangential velocity as:

${\displaystyle \mathbf {v} _{\perp }={\boldsymbol {\omega }}\times \mathbf {r} }$

Spin angular velocity of a rigid body or reference frame[edit source]

Given a rotating frame of three unit coordinate vectors, all the three must have the same angular speed at each instant. In such a frame, each vector may be considered as a moving particle with constant scalar radius.

The rotating frame appears in the context of rigid bodies, and special tools have been developed for it: the spin angular velocity may be described as a vector or equivalently as a tensor.

Consistent with the general definition, the spin angular velocity of a frame is defined as the orbital angular velocity of any of the three vectors (same for all) with respect to its own center of rotation. The addition of angular velocity vectors for frames is also defined by the usual vector addition (composition of linear movements), and can be useful to decompose the rotation as in a gimbal. All components of the vector can be calculated as derivatives of the parameters defining the moving frames (Euler angles or rotation matrices). As in the general case, addition is commutative: ${\displaystyle \omega _{1}+\omega _{2}=\omega _{2}+\omega _{1}}$.

By Euler's rotation theorem, any rotating frame possesses an instantaneous axis of rotation, which is the direction of the angular velocity vector, and the magnitude of the angular velocity is consistent with the two-dimensional case.

If we choose a reference point ${\displaystyle {\boldsymbol {R}}}$ fixed in the rigid body, the velocity ${\displaystyle {\dot {\boldsymbol {r}}}}$ of any point in the body is given by

${\displaystyle {\dot {\boldsymbol {r}}}={\dot {\boldsymbol {R}}}+{\boldsymbol {\omega }}\times ({\boldsymbol {r}}-{\boldsymbol {R}})}$

Components from the basis vectors of a body-fixed frame[edit source]

Consider a rigid body rotating about a fixed point O. Construct a reference frame in the body consisting of an orthonormal set of vectors ${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}}$ fixed to the body and with their common origin at O. The angular velocity vector of both frame and body about O is then

${\displaystyle {\boldsymbol {\omega }}=\left({\dot {\mathbf {e} }}_{1}\cdot \mathbf {e} _{2}\right)\mathbf {e} _{3}+\left({\dot {\mathbf {e} }}_{2}\cdot \mathbf {e} _{3}\right)\mathbf {e} _{1}+\left({\dot {\mathbf {e} }}_{3}\cdot \mathbf {e} _{1}\right)\mathbf {e} _{2},}$

where ${\displaystyle {\dot {\mathbf {e} }}_{i}={\frac {d\mathbf {e} _{i}}{dt}}}$ is the time rate of change of the frame vector ${\displaystyle \mathbf {e} _{i},i=1,2,3,}$ due to the rotation.

Note that this formula is incompatible with the expression

${\displaystyle {\boldsymbol {\omega }}={\frac {\mathbf {r} \times \mathbf {v} }{r^{2}}}.}$

as that formula defines only the angular velocity of a single point about O, while the formula in this section applies to a frame or rigid body. In the case of a rigid body a single ${\displaystyle {\boldsymbol {\omega }}}$ has to account for the motion of all particles in the body.

Components from Euler angles[edit source]

Diagram showing Euler frame in green

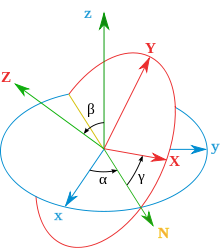
The components of the spin angular velocity pseudovector were first calculated by Leonhard Euler using his Euler angles and the use of an intermediate frame:

• One axis of the reference frame (the precession axis)
• The line of nodes of the moving frame with respect to the reference frame (nutation axis)
• One axis of the moving frame (the intrinsic rotation axis)

Euler proved that the projections of the angular velocity pseudovector on each of these three axes is the derivative of its associated angle (which is equivalent to decomposing the instantaneous rotation into three instantaneous Euler rotations). Therefore:^[5]

${\displaystyle {\boldsymbol {\omega }}={\dot {\alpha }}\mathbf {u} _{1}+{\dot {\beta }}\mathbf {u} _{2}+{\dot {\gamma }}\mathbf {u} _{3}}$

This basis is not orthonormal and it is difficult to use, but now the velocity vector can be changed to the fixed frame or to the moving frame with just a change of bases. For example, changing to the mobile frame:

${\displaystyle {\boldsymbol {\omega }}=({\dot {\alpha }}\sin \beta \sin \gamma +{\dot {\beta }}\cos \gamma ){\hat {\mathbf {i} }}+({\dot {\alpha }}\sin \beta \cos \gamma -{\dot {\beta }}\sin \gamma ){\hat {\mathbf {j} }}+({\dot {\alpha }}\cos \beta +{\dot {\gamma }}){\hat {\mathbf {k} }}}$

where ${\displaystyle {\hat {\mathbf {i} }},{\hat {\mathbf {j} }},{\hat {\mathbf {k} }}}$ are unit vectors for the frame fixed in the moving body. This example has been made using the Z-X-Z convention for Euler angles.^{[citation needed]}

Ptolemy

From Wikipedia, the free encyclopedia

Jump to navigationJump to search

For other uses, see Ptolemy (name), Ptolemy (disambiguation), and Ptolemaeus (disambiguation).

Ptolemy
Κλαύδιος Πτολεμαῖος
Ptolemy "the Alexandrian", as depicted in a 16th-century engraving.[1]
Born	c. 100 AD[2] Egypt, Roman Empire
Died	c. 170 (aged 69–70) AD[2] Alexandria, Egypt, Roman Empire
Citizenship	Roman; ethnicity: Greco-Egyptian
Known for	Ptolemaic universe Ptolemy's world map Ptolemy's intense diatonic scale Ptolemy's table of chords Ptolemy's inequality Ptolemy's theorem Equant Evection Quadrant
Scientific career
Fields	Astronomy, Geography, Astrology, Optics
Influences	Aristotle Hipparchus
Influenced	Theon of Alexandria Abu Ma'shar Nicolaus Copernicus

Claudius Ptolemy (/ˈtɒləmi/; Greek: Πτολεμαῖος, Ptolemaios; Latin: Claudius Ptolemaeus; c. 100 – c. 170 AD)^[2] was a mathematician, astronomer, astrologer, geographer, and music theorist,^[3] who wrote about a dozen scientific treatises, three of which were of importance to later Byzantine, Islamic, and Western European science. The first is the astronomical treatise now known as the Almagest, although it was originally entitled the Mathēmatikē Syntaxis or Mathematical Treatise, and later known as The Greatest Treatise. The second is the Geography, which is a thorough discussion on maps and the geographic knowledge of the Greco-Roman world. The third is the astrological treatise in which he attempted to adapt horoscopic astrology to the Aristotelian natural philosophy of his day. This is sometimes known as the Apotelesmatika (lit. "On the Effects") but more commonly known as the Tetrábiblos, from the Koine Greek meaning "Four Books", or by its Latin equivalent Quadripartite.

Unlike most ancient Greek mathematicians, Ptolemy's writings (foremost the Almagest) never ceased to be copied or commented upon, both in Late Antiquity and in the Middle Ages.^[4] However, it is likely that only a few truly mastered the mathematics necessary to understand his works, as evidenced particularly by the many abridged and watered-down introductions to Ptolemy's astronomy that were popular among the Arabs and Byzantines alike.^[5][6]